스택(Stack - dfs), 큐(queuebfs) 그리고 덱(Deque) 개요

2023-03-17 7 분 소요

스택, 큐, 덱의 정의

우선 스택, 큐, 덱은 자료구조에서 데이터가 어떤 규칙에따라 정리되는지의 차이로 구분되는 자료구조들이다.

주로 선입 선출(FIFO, First in first out), 후입선출(LIFO, Last in first out) , 중간 삽입 등의 데이터 삽입, 추출 방식에 의해 구분되며 각각 DFS, BFS 와 같은 탐색 알고리즘에 적용되고있다.

관련 자료

스택 Stack

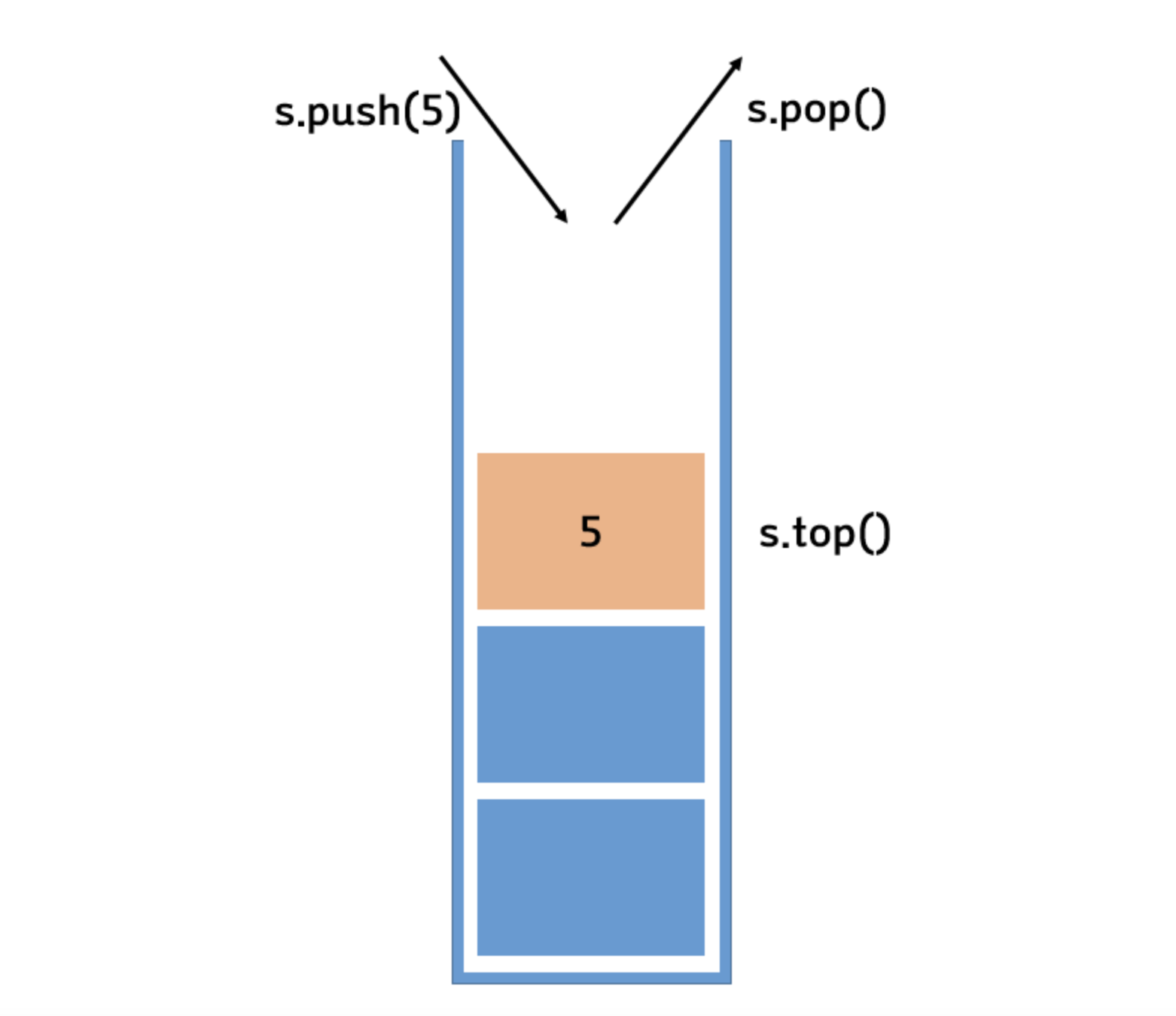
먼저 스택은 한 쪽 끝에서만 자료를 넣고 빼는 작업이 이루어지는 자료구조이다. LIFO (Last In First Out) 방식으로 동작하며 가장 최근에 스택에 삽입된 자료의 위치를 top 이라 한다.

스택의 stack.push 는 top 에 새로운 데이터를 추가하고, stack.pop 은 가장 최근에 삽입된 데이터가 스택에서 삭제된다.

스택의 맨 위 요소, top 에만 접근이 가능하기 때문에 top 이 아닌 위치의 데이터에 대한 접근, 삽입, 삭제는 모두 불가능하다.

스택이 비어있을 때 stack.pop을 시도하는 것을 stack underflow 라 하고 스택의 크기가 비어있을 때 stack.push 를 시도할 때 stack overflow 가 발생한다.

시간 복잡도

top 위치의 데이터에 바로 접근이 가능하기 때문에 데이터 삽입, 삭제의 시간 복잡도는 O(1) 이다.

장단점

top 을 통해 접근하기 때문에 데이터 접근, 삽입, 삭제가 빠르다
top 위치 이외의 데이터에 접근할 수 없기 때문에 탐색이 불가능하다. 탐색하려면 모든 데이터를 꺼내면서 진행해야 한다.

활용

재귀 알고리즘
DFS 알고리즘
작업 실행 취소와 같은 역추적 작업이 필요할 때
괄호 검사, 후위 연산법, 문자열 역순 출력 등

큐 Queue

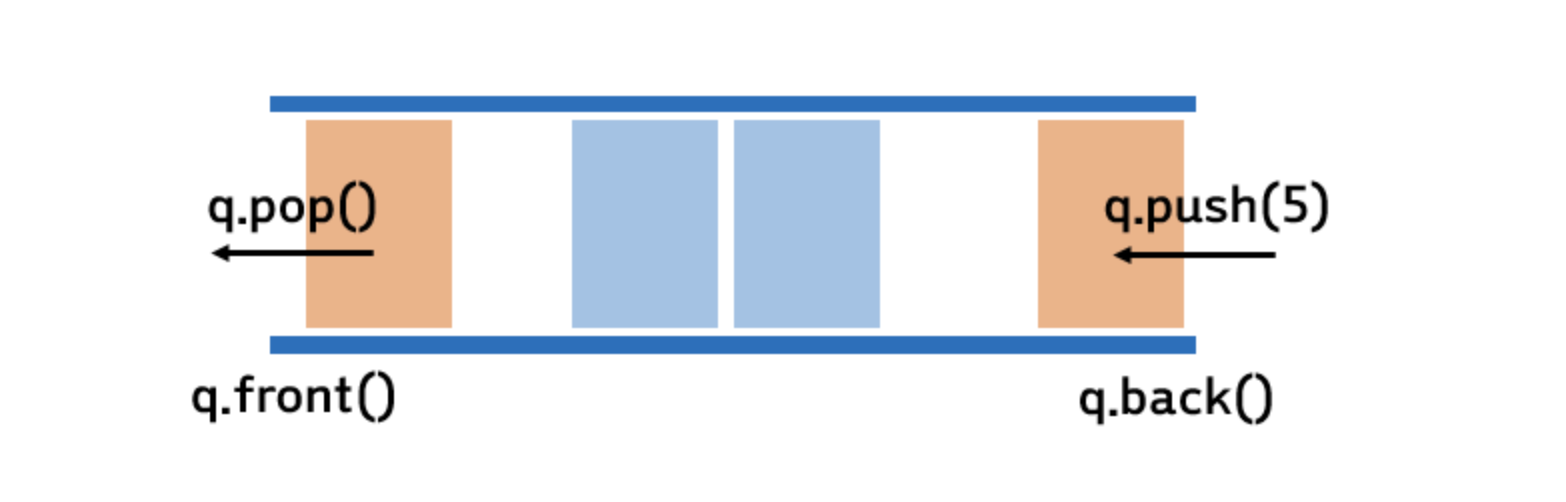
한쪽에서만 데이터의 삽입 삭제가 이루어졌던 스택과 달리 큐는 양쪽 끝에서 데이터의 삽입과 삭제가 각각 이루어진다. FIFO (First In First Out) 으로 동작하며 데이터가 삽입되는 곳을 rear, 데이터가 제거되는 곳을 front 라 한다. 데이터를 삭제하기 전에는 큐가 empty 한지, 큐에 데이터를 추가하려 할 때는 큐가 full 인지 확인 후 진행해야 한다.

선형 큐 Linear Queue

선형 배열을 사용하여 구현된 큐
삽입을 위해서는 계속해서 요소들을 이동시켜야 함
front, rear 는 증가만 하는 방식, 실제로는 front 앞쪽에 공간이 있더라도 삽입할 수 없는 경우가 발생할 수 있음

원형 큐 Circular Queue

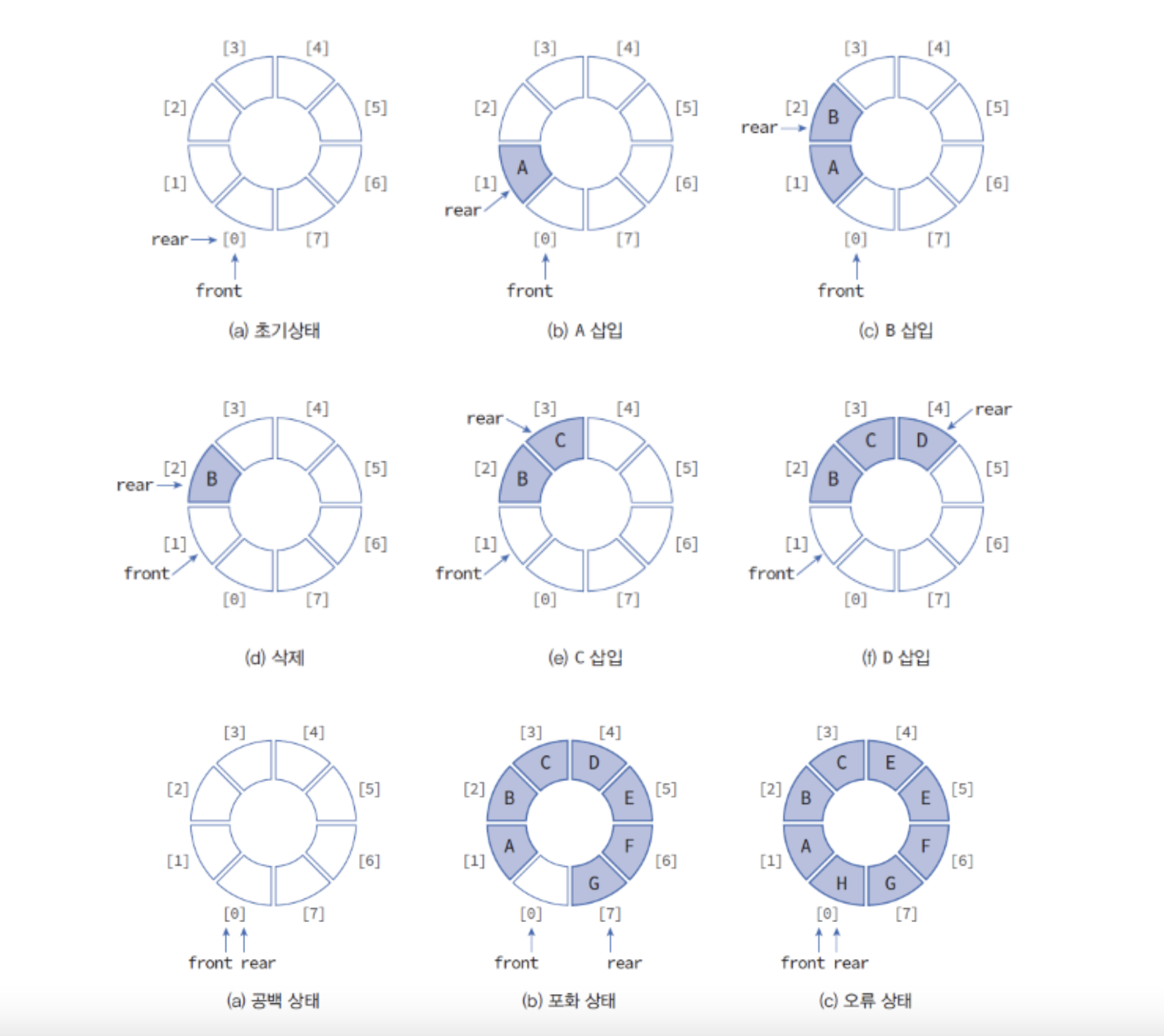
선형 큐의 단점을 보완
front = 맨 첫번째 요소 바로 앞을 가리킴
rear = 마지막 요소 가리킴
큐 empty 상태 : front == rear
큐 full 상태 : front == (rear+1) % MAX_QUEUE_SIZE
공백 상태와 포화 상태를 구분하기 위해 하나의공간을 비워둠

시간 복잡도

큐 역시 front, rear 의 위치로 데이터 삽입 삭제가 바로 이루어지기 때문에 원소 삽입, 삭제의 시간 복잡도는 O(1) 이다.

장단점

데이터 접근, 삽입, 삭제가 빠르다.
큐 역시 스택과 마찬가지로 중간에 위치한 데이터에 대한 접근이 불가능하다.

활용

데이터를 입력된 순서대로 처리해야 할 때
BFS 알고리즘
프로세스 관리
대기 순서 관리

덱 Deque

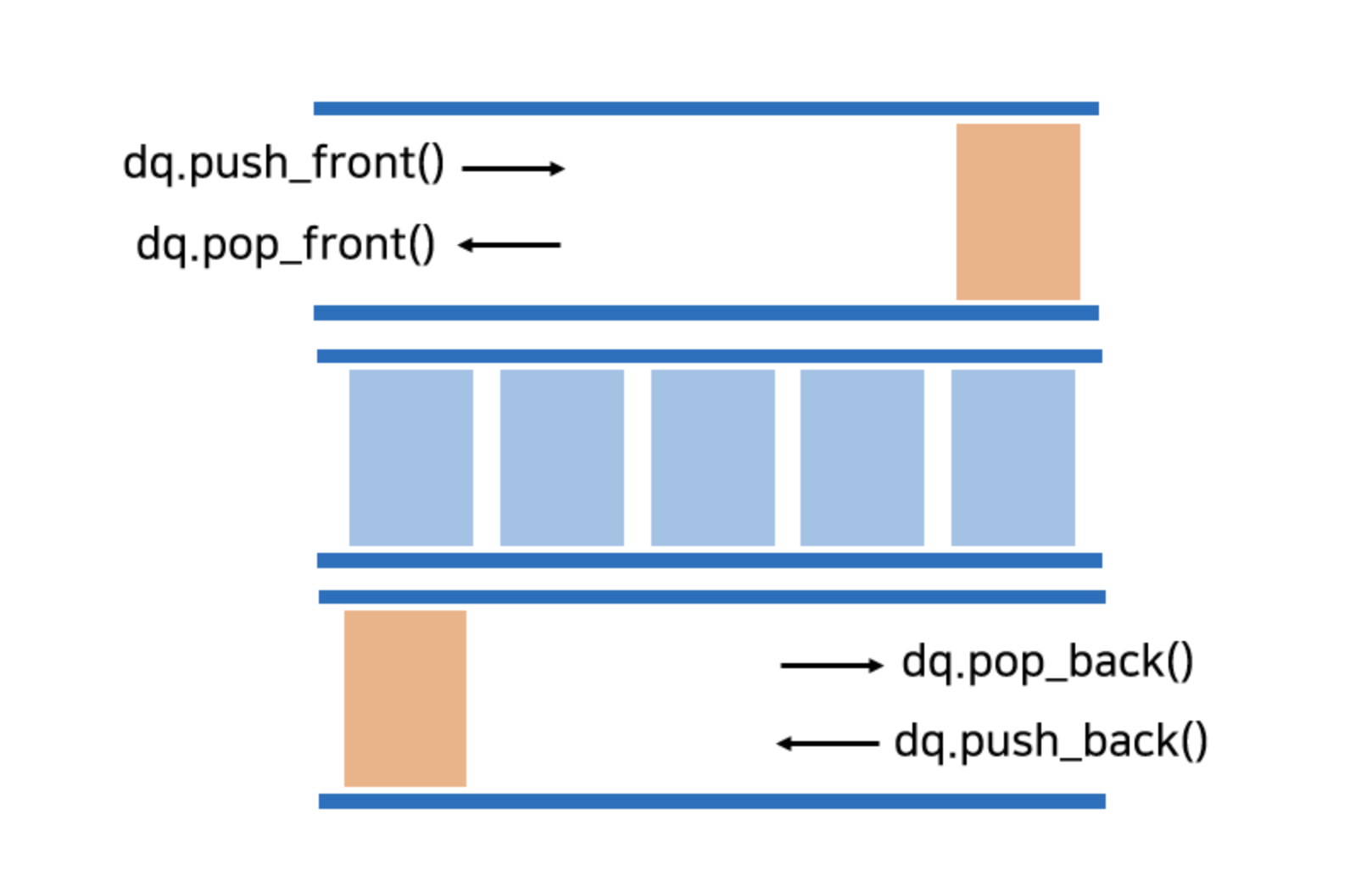
Deque 는 Double - Ended Queue 의 줄임말이다!
한쪽에서만 삽입, 다른 한쪽에서만 삭제가 가능했던 큐와 달리 양쪽 front, rear 에서 삽입 삭제가 모두 가능한 큐를 의미하는 자료구조이다.

연속적인 메모리를 기반으로 하는 시퀀스 컨테이너 이고 선언 이후 크기를 줄이거나 늘릴 수 있는 가변적 크기를 갖는다.

또한 중간에 데이터가 삽입될 때 다른 요소들을 앞, 뒤로 밀 수 있다. vector 보다는 좋은 성능을 가지지만 앞, 뒤에서의 삽입 삭제 성능에 비해 중간에 삽입 삭제 하는 것은 성능이 좋지 않다!

시간 복잡도

삽입 삭제 연산은 마찬가지로 O(1) 의 시간 복잡도를 가지고, 스택/큐와 달리 index 를 통해 요소들에 탐색이 가능하므로 이 역시 O(1) 의 시간 복잡도를 가진다.

장단점

데이터의 삽입 삭제가 빠르고 앞, 뒤에서 삽입 삭제가 모두 가능하다
가변적 크기
index 를 통해 임의의 원소에 바로 접근이 가능하고
새로운 원소 삽입 시, 메모리를 재할당하고 복사하지 않고 새로운 단위의 메모리 블록을 할당하여 삽입한다.
중간에서의 삽입 삭제가 어렵고
스택, 큐에 비해 비교적 구현이 어렵다.

💡 vector 에 비해 deque가 메모리 추가 할당이 더 저렴한 이유!
vector는 데이터를 저장하는 버퍼를 1차원 배열 형태로 관리하기 때문에 vector 는 메모리를 추가로 할당할 경우 기존 메모리 영역의 2배만큼 메모리를 추가로 할당하고 기존의 요소를 복사한다.

deque 는 chunk 를 이용해 관리한다. chunk 는 메모리 영역 군데군데에 흩어져 있고 컨테이너에서 내부적으로 chunk 에 바로 접근이 가능하도록 인터페이스를 제공한다. 때문에 처음에 할당받은 chunk 를 모두 사용중이라면 deque 는 새로운 chunk 를 하나 만드는 것 만으로 메모리 추가 할당이 완료된다!

활용

데이터를 앞, 뒤쪽에서 모두 삽입 삭제하는 과정이 필요한 경우
데이터의 크기가 가변적일 때

파이썬 코딩 테스트에서 자주 사용되는 데큐(deque)입니다.

  from collections import deque

이렇게 불러올 수 있습니다.

deque를 사용하면 얻는 장점

엄격한 리스트를 만들 수 있다.
속도가 리스트에 비해 굉장히 빠르다. List = O(n), deque = O(1)
당연하지만 큐작업이 훨씬 편해진다.

1. 큐(QUEUE)에 대한 이해.

큐는 기본적으로 선입 선출 (FIFO : First In First Out)구조입니다.

예시로는 다음이 있습니다.

프린터기 : 프린터기는 먼저 인쇄를 누른 것부터 차례대로 작동합니다.
은행 대기표 : 은행에서는 먼저 대기표를 뽑은 사람부터 차례대로 서비스를 진행합니다.

deque 함수는 큐에 제한되어 있는 선입선출 제한을 풀어서, 더 여러곳에 사용할 수 있도록 한 함수입니다.

2. deque 사용하기

>>> from collections import deque
>>> data = [1, 2, 3, 4, 5]
>>> d = deque(data)
>>> print(d)


deque([1, 2, 3, 4, 5])

함수 목록은 다음을 참조해주세요.

함수 목록:

append
appendleft
clear
copy
count
extend
extendleft
index
insert
maxlen
pop
popleft
remove
reverse
rotate

보시면 아시겠지만, 리스트 함수와 굉장히 유사합니다.

여기서 눈여겨 볼 함수는 다음과 같습니다.

appendleft : 왼쪽에 개체를 추가합니다.
extendleft : 왼쪽에 리스트를 연장합니다.
maxlen : 큐의 길이를 반환합니다.
popleft : 큐의 맨 왼쪽에 있는 개체를 반환합니다.
rotate : 큐를 회전합니다.

로테이트는 처음 접하시면 생소하실 것입니다.

>>> d = deque([1, 2, 3, 4, 5])
>>> print(d)
>>> d.rotate(2)
>>> print(d)
>>> d.rotate(-2)
>>> print(d)

deque([1, 2, 3, 4, 5])
deque([4, 5, 1, 2, 3])
deque([1, 2, 3, 4, 5])

큐 [1 ,2 ,3 ,4 ,5]가 오른쪽에서 왼쪽 방향으로 2 회전하여

[4, 5, 1, 2, 3]이 되었습니다.

이번에는 반대로 -2로 회전하여

[1 ,2 ,3 ,4 ,5]가 되었습니다.

[Python] 파이썬으로 bfs, dfs 구현해보기

BFS, DFS

우선 BFS, DFS가 뭔지부터 알아보자.

BFS, DFS 개념

다음과 같은 그래프가 있다고하자. (PPT로 그린거라 좀 허접해도 양해바람)

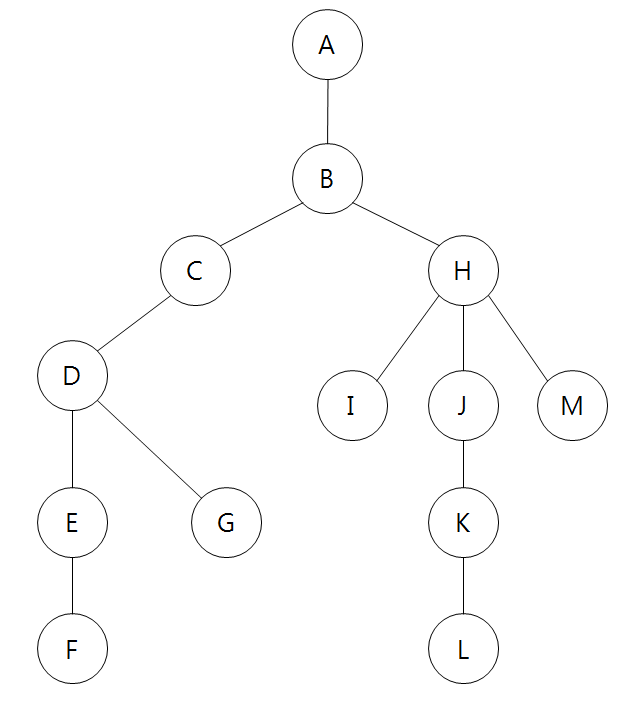
A부터 시작해서 모든 노드를 순회하는 방법은 다음과 같이 크게 두가지가 있을 것이다.

그림과 비교하면서 눈으로 잘 따라가보자.

A - B - C - H - D - I - J - M - E - G - K - F - L
A - B- C - D - E - F - G - H - I - J - K - L - M

1번 방식은 한 단계씩 나아가면서 해당 노드와 같은 레벨에 있는 노드들(즉, 형제 노드들)을 먼저 순회하는 방식이다.

이러한 방식을 Breath First Search (너비 우선 탐색, BFS) 라고 한다.

2번 방식은 한 노드의 자식을 타고 끝까지 순회한 다음에, 다시 돌아와서 다른 형제의 자식을 타고 내려가며 순회하는 방식이다.

방문 순서와 그림을 대조해서 보면 이해가 갈것이다.

이러한 방식은 Depth First Search (깊이 우선 탐색, DFS) 라고 한다.

파이썬으로 구현해보기

그래프를 다시 가져와보자.

파이썬에서 BFS, DFS를 구현하기 위해서는 우선 그래프를 코드로 표현해야한다.

한 노드를 중심으로 연결관계가 있는 노드를 모두 표현해주면 될 것이다.

여러가지 방법이 있겠지만, 딕셔너리와 리스트를 사용해 표현해보자.

graph = {
    'A': ['B'],
    'B': ['A', 'C', 'H'],
    'C': ['B', 'D'],
    'D': ['C', 'E', 'G'],
    'E': ['D', 'F'],
    'F': ['E'],
    'G': ['D'],
    'H': ['B', 'I', 'J', 'M'],
    'I': ['H'],
    'J': ['H', 'K'],
    'K': ['J', 'L'],
    'L': ['K'],
    'M': ['H']
}

그림이랑 코드를 잘 비교해서 보면 대충 모양새가 이해될것이다.

Python - BFS

우선 BFS를 먼저 구현해보자.

def bfs(graph, start_node):
   visit = list()
   queue = list()
  4
   queue.append(start_node)
  6
   while queue:
       node = queue.pop(0)
       if node not in visit:
           visit.append(node)
           queue.extend(graph[node])
 12
   return visit

앞서 만든 그래프와 시작 노드를 받아서 BFS 방식으로 그래프를 순회하는 함수이다.

(2~3) 방문했던 노드 목록을 차례대로 저장할 리스트와, 다음으로 방문할 노드의 목록을 차례대로 저장할 리스트(큐)를 만들어주자.

(5) 우선 맨 처음에는 당연히 시작 노드를 큐에 넣어준다.

(7) 큐의 목록이 바닥날때까지(더 이상 방문할 노드가 없을 때까지) loop를 돌려준다.

(8) 큐의 맨 앞에있는 노드를 꺼내온다.

(9) 해당 노드가 아직 방문 리스트에 없다면,

(10) 방문 리스트에 추가해주고,

(11) 해당 노드의 자식 노드들을 큐에 추가해준다.

자식 노드들을 큐에 추가하면서 큐에 먼저 추가됐던 노드부터 순차적으로 방문하게되면 결국엔 BFS형태로 순회하게 된다.

코드는 별로 어렵지 않지만, 처음 보면 직관적으로 와닿지는 않을것이다.

맨 아래쪽에 전체 코드를 첨부했으니,

코드를 복사해서 while문 안에 visit와 queue를 출력하며 한 단계씩 과정을 살펴보면 보다 쉽게 이해가 될 것이다.

Python - DFS

이번엔 DFS를 구현해보자.

코드 기준으로 봤을때 DFS는 BFS와 거의 똑같고, queue대신 stack을 사용한다는 점만 다르다.

def dfs(graph, start_node):
   visit = list()
   stack = list()
  4
   stack.append(start_node)
  6
   while stack:
       node = stack.pop()
       if node not in visit:
           visit.append(node)
           stack.extend(graph[node])
 12
   return visit

queue의 변수명이 stack으로 바뀌었고, 8번 라인에서 pop(0) 을 하던 부분이 pop() 으로 바뀌었다.

리스트에서 pop()을 하게되면 맨 마지막에 넣었던 아이템을 가져오게 되므로 stack과 동일하게 동작하게 된다.

반대로 pop(0)을 하게되면 맨 앞에있는 요소를 가져오므로 queue와 동일하게 동작했던 것이다.

전체 코드

마지막으로 공부하면서 정리한 전체 코드를 공유한다.

나도 100% 이해한채로 구현했다고 하기엔 어려워서,

혹시 개선할 부분이 있거나 잘못 구현된 부분이 있다면 꼭 댓글을 달아줬으면 좋겠다!

def bfs(graph, start_node):
    visit = list()
    queue = list()

    queue.append(start_node)

    while queue:
        node = queue.pop(0)
        if node not in visit:
            visit.append(node)
            queue.extend(graph[node])

    return visit


def dfs(graph, start_node):
    visit = list()
    stack = list()

    stack.append(start_node)

    while stack:
        node = stack.pop()
        if node not in visit:
            visit.append(node)
            stack.extend(graph[node])

    return visit


if __name__ == "__main__":
    graph = {
        'A': ['B'],
        'B': ['A', 'C', 'H'],
        'C': ['B', 'D'],
        'D': ['C', 'E', 'G'],
        'E': ['D', 'F'],
        'F': ['E'],
        'G': ['D'],
        'H': ['B', 'I', 'J', 'M'],
        'I': ['H'],
        'J': ['H', 'K'],
        'K': ['J', 'L'],
        'L': ['K'],
        'M': ['H']
    }

    print(bfs(graph, 'A'))
    print(dfs(graph, 'A'))

나 또한 이제 공부를 막 시작한지라 많이 부족하지만, 대강의 개념을 잡는 정도로 누군가에게 도움이 되었으면 좋겠다.

추가 (2019.09.16)

사실 이 코드는 성능면에서 개선해야할 부분이 많은 코드입니다.

예를들어 python의 list는 stack과 유사하게 동작하기때문에,

bfs 코드에서 변수 queue는 list보다 말그대로 queue 모듈을 사용해 구현하는 것이 효율적입니다.

또한,

이미 방문한 노드를 저장하는 visit 변수는 list보다는 dict로 구현하는 것이 탐색시 보다 유리합니다.

좀 더 자세한 내용은 댓글에 몇 분이 코드와 함께 친절히 댓글을 달아주셨습니다.

해당 포스팅에 대한 모든 분들의 기여에 진심으로 감사드립니다.

누구나 볼 수 있도록 공개된 코드인만큼 앞으로는 더욱 신중히 작성할 수 있도록 신경쓰겠습니다.

참고문헌

https://velog.io/@nnnyeong/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%EC%8A%A4%ED%83%9D-Stack-%ED%81%90-Queue-%EB%8D%B1-Deque

[[python] 파이썬으로 bfs, dfs 구현해보기

코딩장이](https://itholic.github.io/python-bfs-dfs/)

Twitter Facebook LinkedIn

스택(Stack - dfs), 큐(queuebfs) 그리고 덱(Deque) 개요

스택, 큐, 덱의 정의

관련 자료

스택 Stack

시간 복잡도

장단점

활용

큐 Queue

선형 큐 Linear Queue

원형 큐 Circular Queue

시간 복잡도

장단점

활용

덱 Deque

시간 복잡도

장단점

활용

1. 큐(QUEUE)에 대한 이해.

2. deque 사용하기

[Python] 파이썬으로 bfs, dfs 구현해보기

BFS, DFS

BFS, DFS 개념

파이썬으로 구현해보기

Python - BFS

Python - DFS

전체 코드

추가 (2019.09.16)

참고문헌

공유하기

참고

파이썬 (Python) - 깊은 복사 (Deep Copy)

DFS+BFS 필수 문제 - 촌수계산

파이썬 입력 받기(input VS sys.stdin.readline 차이점)

DFS+BFS 필수 문제 - 단지번호붙이기